Can an iterative draft–revise solver that repeatedly updates a latent scratchpad outperform far larger autoregressive LLMs on ARC-AGI? Samsung SAIT (Montreal) has released Tiny Recursive Model (TRM)—a two-layer, ~7M-parameter recursive reasoner that reports 44.6–45% test accuracy on ARC-AGI-1 and 7.8–8% on ARC-AGI-2, surpassing results reported for substantially larger language models such as DeepSeek-R1, o3-mini-high, and Gemini 2.5 Pro on the same public evaluations. TRM also improves puzzle benchmarks Sudoku-Extreme (87.4%) and Maze-Hard (85.3%) over the prior Hierarchical Reasoning Model (HRM, 27M params), while using far fewer parameters and a simpler training recipe.
What’s exactly is new?
TRM removes HRM’s two-module hierarchy and fixed-point gradient approximation in favor of a single tiny network that recurses on a latent “scratchpad” (z) and a current solution embedding (y):
Single tiny recurrent core. Replaces HRM’s two-module hierarchy with one 2-layer network that jointly maintains a latent scratchpad 𝑧 z and a current solution embedding 𝑦 y. The model alternates: think: update 𝑧 ← 𝑓 ( 𝑥 , 𝑦 , 𝑧 ) z←f(x,y,z) for 𝑛 n inner steps; act: update 𝑦 ← 𝑔 ( 𝑦 , 𝑧 ) y←g(y,z).
Deeply supervised recursion. The think→act block is unrolled up to 16 times with deep supervision and a learned halting head used during training (full unroll at test time). Signals are carried across steps via (y,z)(y, z)(y,z).
Full backprop through the loop. Unlike HRM’s one-step implicit (fixed-point) gradient approximation, TRM backpropagates through all recursive steps, which the research team find essential for generalization.
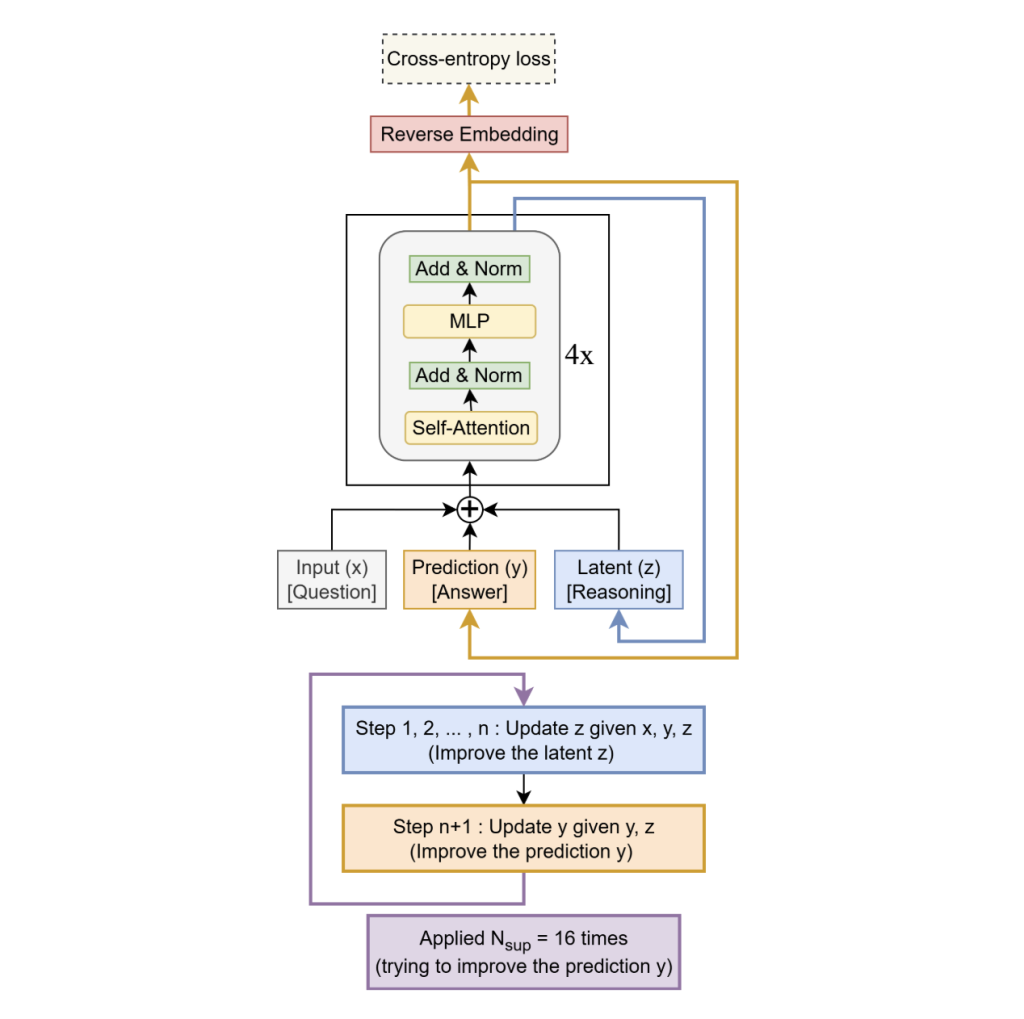
Architecturally, the best-performing setup for ARC/Maze retains self-attention; for Sudoku’s small fixed grids, the research team swap self-attention for an MLP-Mixer-style token mixer. A small EMA (exponential moving average) over weights stabilizes training on limited data. Net depth is effectively created by recursion (e.g., T = 3, n = 6) rather than stacking layers; in ablations, two layers generalize better than deeper variants at the same effective compute.
Understanding the Results
ARC-AGI-1 / ARC-AGI-2 (two tries): TRM-Attn (7M): 44.6% / 7.8% vs HRM (27M): 40.3% / 5.0%. The research team-reported LLM baselines: DeepSeek-R1 (671B) 15.8% / 1.3%, o3-mini-high 34.5% / 3.0%, Gemini 2.5 Pro 37.0% / 4.9%; larger bespoke Grok-4 entries are higher (66.7–79.6% / 16–29.4%).
Sudoku-Extreme (9×9, 1K train / 423K test): 87.4% with attention-free mixer vs HRM 55.0%.
Maze-Hard (30×30): 85.3% vs HRM 74.5%.
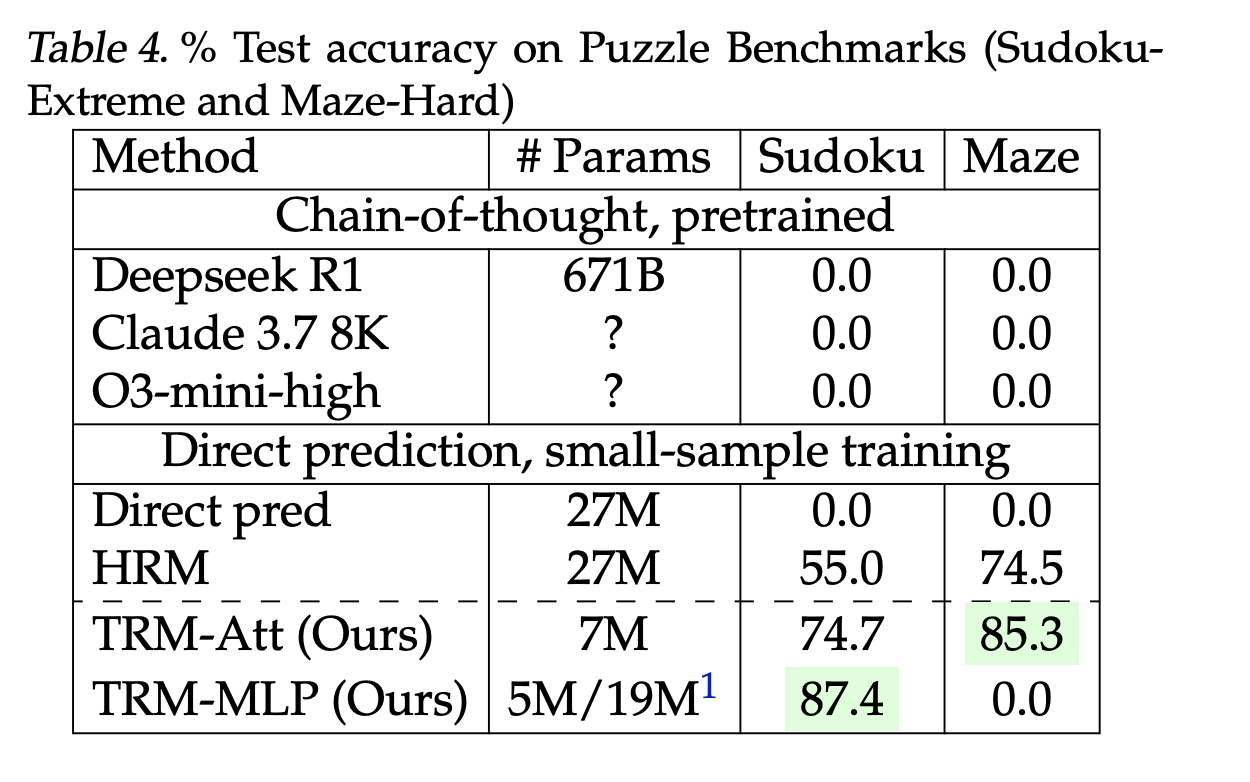

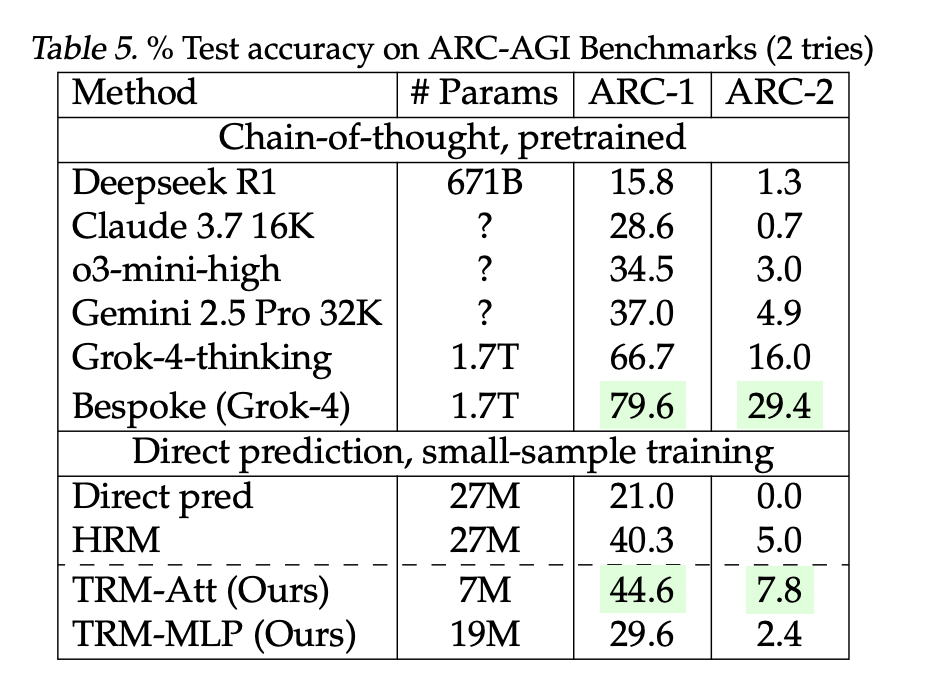

These are direct-prediction models trained from scratch on small, heavily augmented datasets—not few-shot prompting. ARC remains the canonical target; broader leaderboard context and rules (e.g., ARC-AGI-2 grand-prize threshold at 85% private set) are tracked by the ARC Prize Foundation.
Why a 7M model can beat much larger LLMs on these tasks?
Decision-then-revision instead of token-by-token: TRM drafts a full candidate solution, then improves it via latent iterative consistency checks against the input—reducing exposure bias from autoregressive decoding on structured outputs.
Compute spent on test-time reasoning, not parameter count: Effective depth arises from recursion (emulated depth ≈ T·(n+1)·layers), which the researchers show yields better generalization at constant compute than adding layers.
Tighter inductive bias to grid reasoning: For small fixed grids (e.g., Sudoku), attention-free mixing reduces overcapacity and improves bias/variance trade-offs; self-attention is kept for larger 30×30 grids.
Key Takeaways
Architecture: A ~7M-param, 2-layer recursive solver that alternates latent “think” updates 𝑧 ← 𝑓 ( 𝑥 , 𝑦 , 𝑧 ) z←f(x,y,z) and an “act” refinement 𝑦 ← 𝑔 ( 𝑦 , 𝑧 ) y←g(y,z), unrolled up to 16 steps with deep supervision; gradients are propagated through the full recursion (no fixed-point/IFT approximation).
Results: Reports ~44.6–45% on ARC-AGI-1 and ~7.8–8% on ARC-AGI-2 (two-try), surpassing several much larger LLMs as cited in the research paper’s comparison (e.g., Gemini 2.5 Pro, o3-mini-high, DeepSeek-R1) under the stated eval protocol.
Efficiency/Pattern: Demonstrates that allocating test-time compute to recursive refinement (depth via unrolling) can beat parameter scaling on symbolic-geometric tasks, offering a compact, from-scratch recipe with publicly released code.
This research demonstrates a ~7M-parameter, two-layer recursive solver that unrolls up to 16 draft-revise cycles with ~6 latent updates per cycle and reports ~45% on ARC-AGI-1 and ~8% (two-try) on ARC-AGI-2. The research team released code on GitHub. ARC-AGI remains unsolved at scale (target 85% on ARC-AGI-2), so the contribution is an architectural efficiency result rather than a general reasoning breakthrough.
Check out the Technical Paper and GitHub Page. Feel free to check out our GitHub Page for Tutorials, Codes and Notebooks. Also, feel free to follow us on Twitter and don’t forget to join our 100k+ ML SubReddit and Subscribe to our Newsletter. Wait! are you on telegram? now you can join us on telegram as well.
Asif Razzaq is the CEO of Marktechpost Media Inc.. As a visionary entrepreneur and engineer, Asif is committed to harnessing the potential of Artificial Intelligence for social good. His most recent endeavor is the launch of an Artificial Intelligence Media Platform, Marktechpost, which stands out for its in-depth coverage of machine learning and deep learning news that is both technically sound and easily understandable by a wide audience. The platform boasts of over 2 million monthly views, illustrating its popularity among audiences.

